
Our 2 disc case builds on this by using the buffer tower to store the top disc, allowing us to simply solve the single disc case for the remaining disc. This single disc case is our "base case" in recursion terms. Our solution for 2 discs ( N = 2) reused our solution for a single disc ( N = 1).
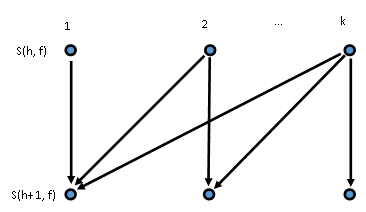
but what about N discs? Instead, can we break these larger cases down into cases we've already solved? Yes.

How about 3 or 4 discs? We could handcraft a solution for every case.
#Hanoi towers function how to
We now know how to solve this for both a single disc as well as 2 discs. Towers_of_hanoi_1_disc(origin, destination) # Move the second disc to the destinationĭestination.append(buffer.pop()) # Move the first disc to the destination Scale up with recursion Our function for 2 discs looks looks like this: # Move 2 discs from the origin to the destination tower def towers_of_hanoi_2_discs( origin, buffer, destination):īuffer.append(origin.pop()) # Move the first disc into our buffer

Move the small disc from the buffer tower onto the destination tower.Move the large (bottom) disc from the origin tower directly to the destination tower.Move the small (top) disc from the origin tower onto the buffer tower (put it in storage).We can think of this tower as our buffer tower, which can act as our temporary storage. How can we build on top of this to solve for 2 discs? First we can reintroduce our friend, the third tower. Mind blowing, isn't it? To move the disc to the destination, we can simply pop it off our origin tower, and append it to the destination tower. # Move a single disc from the origin to the destination def towers_of_hanoi_1_disc( origin, destination): This function can ignore the third tower for now. In the single disc case, our origin tower contains, and the destination tower contains, as it's currently empty. Each stack contains the discs currently on that tower. Our function can take a stack (or list) for each tower. What's the simplest version of this problem? If we always have three towers and a variable number of disks, then a single disc is the simplest version. How else can you think about this? Start simple This doesn't translate well into an algorithm though. You could just move the discs randomly, following the rules above, until you've managed to move every disk onto the third tower. What do you do with the first disc? Once you've moved this disc, where can you move the second disc? How have you moved closer to solving the puzzle?

Take a moment to think about how you would approach this. A disk cannot be placed on another disk which is smaller than it.The challenge is to move these disks to the third tower, following these rules: The first tower has a set of disks on it which increase in size from top to bottom. Let's start with a quick refresher on the problem. or you're just brushing up on some algorithms, either way, you've come across a question asking you to solve the Towers of Hanoi problem. So there you are, in an interview, palms are sweaty, mum's spaghetti.


 0 kommentar(er)
0 kommentar(er)
